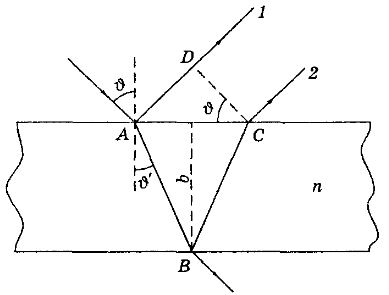
 |
| Рис. 9 |
Заметим, что, кроме этих двух отраженных волн (1 и 2), возникает еще многократное отражение. Однако их вклад практически пренебрежимо мал (см. задачу 5 в разделе 1.3 ``Примеры решения задач''), и мы ограничимся только волнами, возникшими при однократном отражении.
Оптическую разность хода волн 1 и 2 определим, согласно рис. 9, как
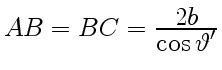 и
и
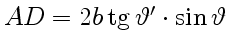 ,
, 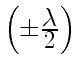 .
Учитывая еще, что
.
Учитывая еще, что
Если отраженные волны 1 и 2 когерентны между собой (а мы об этом позаботимся), то максимумы отражения будут наблюдаться при условии
Меняя угол падения ![]() , мы будем наблюдать
последовательную смену максимумов и минимумов отражения. (Заметим,
что при минимуме отражения наблюдается максимум проходящего через
пластинку света, и наоборот.) Если бы обе отраженные волны были
некогерентными, то такого явления мы не наблюдали бы: по мере
увеличения угла падения интенсивность отраженного света монотонно
уменьшалась бы.
, мы будем наблюдать
последовательную смену максимумов и минимумов отражения. (Заметим,
что при минимуме отражения наблюдается максимум проходящего через
пластинку света, и наоборот.) Если бы обе отраженные волны были
некогерентными, то такого явления мы не наблюдали бы: по мере
увеличения угла падения интенсивность отраженного света монотонно
уменьшалась бы.
Теперь выясним условия, при которых отраженные волны будут когерентными и смогут интерферировать, т. е. выполняются соотношения (22) и (25).
Проиллюстрируем ситуацию с помощью рис. 10. Выделим
в падающей волне некоторую область когерентности
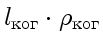 (она слегка затенена на
рисунке) и проследим за ее дальнейшей судьбой. После расщепления
падающей волны расщепится и выделенная область когерентности,
причем так, что в отраженных волнах эти области когерентности
сместятся относительно друг друга рис. 10,a. Если
они при этом перекрываются (на рисунке более темный участок),
интерференция будет наблюдаться и тем более отчетливо, чем больше
степень перекрытия.
(она слегка затенена на
рисунке) и проследим за ее дальнейшей судьбой. После расщепления
падающей волны расщепится и выделенная область когерентности,
причем так, что в отраженных волнах эти области когерентности
сместятся относительно друг друга рис. 10,a. Если
они при этом перекрываются (на рисунке более темный участок),
интерференция будет наблюдаться и тем более отчетливо, чем больше
степень перекрытия.
Нетрудно видеть, что для пластинки с большей толщиной область перекрытия когерентных участков уменьшается рис. 10 b, и интерференция будет наблюдаться все менее отчетливо. Начиная с некоторой толщины пластинки итерференция исчезнет совсем.
Из рис. 10 видно, что смещение расчлененных частей
области когерентности происходит как вдоль распространения волны
(оно не должно превосходить длину когерентности
![]() ), так и поперек распространения волны (смещение
не должно превосходить ширину когерентности
), так и поперек распространения волны (смещение
не должно превосходить ширину когерентности
![]() ). Интерференция будет наблюдаться лишь в том
случае, когда будут удовлетворены оба эти условия. Напомним, что
для лучшей видности мы договорились брать половины значений
). Интерференция будет наблюдаться лишь в том
случае, когда будут удовлетворены оба эти условия. Напомним, что
для лучшей видности мы договорились брать половины значений
![]() и
и
![]() .
.
Перейдем к расчету. Согласно (22), необходимо, чтобы
оптическая разность хода
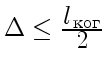 . Следовательно,
. Следовательно,
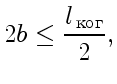
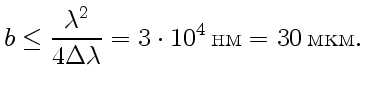
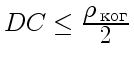 . Из рис.
9 следует, что
. Из рис.
9 следует, что
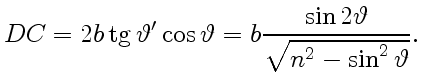
Обратимся к вопросу, что следует понимать под словами «тонкая»
пластинка. Когда говорят, что интерференция происходит при
отражении от тонкой пластинки, то имеют в виду, что ее толщина
меньше (в той или иной степени)
![]() и
и
![]() (если
(если
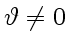 ). Причем — это важно —
при нормальном падении интерференция обеспечивается только
соотношением между толщиной пластинки и
). Причем — это важно —
при нормальном падении интерференция обеспечивается только
соотношением между толщиной пластинки и
![]() .
.
Для солнечного света (
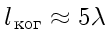 )
пластинка будет тонкой, если ее толщина порядка нескольких длин
волн. Длину когерентности можно увеличить с помощью светофильтров,
соответственно увеличивается и толщина пластинки, которую мы
называем тонкой. Для лазерного же излучения тонкой будет пластинка
в десятки сантиметров и метров (в зависимости от длины
когерентности излучения используемого лазера).
)
пластинка будет тонкой, если ее толщина порядка нескольких длин
волн. Длину когерентности можно увеличить с помощью светофильтров,
соответственно увеличивается и толщина пластинки, которую мы
называем тонкой. Для лазерного же излучения тонкой будет пластинка
в десятки сантиметров и метров (в зависимости от длины
когерентности излучения используемого лазера).
Итак, мы выяснили, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отраженного света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отраженного света. Это можно использовать для получения интерференционной картины в виде привычной системы полос. Достаточно использовать в качестве падающего рассеянный монохроматический свет (он содержит волны, падающие на пластинку одновременно под разными углами), а на пути отраженного света поставить линзу и в ее фокальной плоскости экран (рис. 11).
Максимумы на экране будут располагаться в местах, соответствующих
условию (35). Полоса данного порядка интерференции
обусловлена светом, падающим на пластинку под одним и тем же углом
![]() , но с разных направлений. Поэтому такие полосы
называют полосами равного наклона. При расположении линзы
как показано на рисунке, эти полосы имеют вид концентрических
колец с центром в ее фокусе
, но с разных направлений. Поэтому такие полосы
называют полосами равного наклона. При расположении линзы
как показано на рисунке, эти полосы имеют вид концентрических
колец с центром в ее фокусе ![]() . Порядок интерференции
. Порядок интерференции ![]() растет
с уменьшением угла падения
растет
с уменьшением угла падения ![]() , и в центре картины он
максимален.
, и в центре картины он
максимален.
Поскольку для наблюдения интерференционной картины в данном случае экран помещают в фокальной плоскости линзы, т. е. так, как его располагают для получения на нем изображения бесконечно удаленных предметов, то говорят, что полосы равного наклона локализованы в бесконечности. Роль линзы и экрана может играть хрусталик и сетчатка глаза. В этом случае для наблюдения полос равного наклона глаз нужно аккомодировать (настраивать) так, как при рассмотрении удаленных предметов.
В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цвета тонких пластинок.