 |
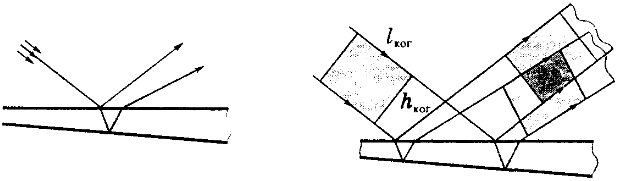
| Рис. 12 |
Выясним прежде всего, где будет локализована интерференционная
картина. Это проще всего сделать с помощью
рис.12, на котором показано, что происходит с
областью когерентности после расщепления волны при отражении от
поверхностей клина. Ясно, что при небольших значениях
![]() и
и
![]() , область перекрытия
когерентных частей отраженных волн локализована в основном вблизи
поверхности клина и становится все более узкой по мере перемещения
в сторону утолщения клина, постепенно исчезая совсем. На рисунке
область локализации несколько затемнена.
, область перекрытия
когерентных частей отраженных волн локализована в основном вблизи
поверхности клина и становится все более узкой по мере перемещения
в сторону утолщения клина, постепенно исчезая совсем. На рисунке
область локализации несколько затемнена.
Так как разность хода лучей, отразившихся от различных участков клина, неодинакова, в области локализации интерференции появятся светлые и темные полосы, параллельные ребру клина. Каждая из таких полос возникает в результате отражений от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
Локализованные вблизи поверхности клина интерференционные полосы можно наблюдать непосредственно глазом, фокусируя его на поверхность клина, либо с помощью линзы, сфокусированной также на поверхность клина. С помощью линзы интерференционную картину с поверхности клина можно отобразить на экран Э, расположенный в плоскости, сопряженной с поверхностью клина.
Полосы равной толщины можно наблюдать в тонкой клиновидной прослойке воздуха между поверхностями двух прозрачных пластинок. Если
направление наблюдения близко к нормальному, то оптическая разность хода лучей, отраженных от поверхностей клина в месте, где ширина зазора
равна ![]() , определяется как
, определяется как
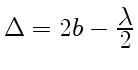 . Там, где
. Там, где
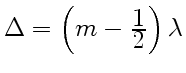 ,
,
![]() , возникают минимумы. Т. е. темные полосы
возникают в тех местах, где толщина зазора
, возникают минимумы. Т. е. темные полосы
возникают в тех местах, где толщина зазора
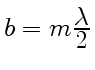 . Переход от одной
полосы к соседней (ширина полосы
. Переход от одной
полосы к соседней (ширина полосы
![]() ) соответствует
изменению толщины зазора на
) соответствует
изменению толщины зазора на
![]() . Каждая полоса
соответствует определенной толщине зазора. Это используют для
проверки качества оптических поверхностей при их шлифовке,
наблюдая в отраженном свете прослойку между контролируемой и
эталонной поверхностями.
. Каждая полоса
соответствует определенной толщине зазора. Это используют для
проверки качества оптических поверхностей при их шлифовке,
наблюдая в отраженном свете прослойку между контролируемой и
эталонной поверхностями.
Измеряя ширину полосы
![]() в монохроматическом свете с
известной длиной волны
в монохроматическом свете с
известной длиной волны ![]() , можно измерить углы порядка 0,1
угл. мин и меньше (см. задачу 4
из раздела 1.4 ``Примеры решения
задач'').
, можно измерить углы порядка 0,1
угл. мин и меньше (см. задачу 4
из раздела 1.4 ``Примеры решения
задач'').
В предыдущих рассуждениях мы принимали во внимание только волны, отраженные от поверхностей воздушного клиновидного зазора, игнорируя волны, отраженные от наружных поверхностей пластинок. Это можно сделать лишь постольку, поскольку толщина пластинок обычно значительно превышает длину когерентности используемого света от обычных источников, и отраженные от этих поверхностей волны оказываются некогерентными.