С электромагнитной волной связан перенос энергии. Плотность потока энергии ![]() можно найти с помощью формулы
можно найти с помощью формулы ![]() , как произведение плотности энергии
, как произведение плотности энергии ![]() на скорость волны
на скорость волны ![]() (см. [ ], гл.1 §1.4).
(см. [ ], гл.1 §1.4).
В обычной изотропной среде с проницаемостями
![]() и
и ![]() плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:
плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:
Умножив ![]() на
на ![]() , получим плотность потока энергии:
, получим плотность потока энергии:
Векторы
![]() и
и
![]() взаимно ортогональны и образуют с направлением распространения волны правовинтовую систему. Значит, направление вектора
взаимно ортогональны и образуют с направлением распространения волны правовинтовую систему. Значит, направление вектора
![$ [\strut\mathbf{EH}]$](img98.gif) совпадает с направлением переноса энергии, а модуль этого вектора равен
совпадает с направлением переноса энергии, а модуль этого вектора равен 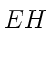 . Поэтому вектор плотности потока электромагнитной энергии
. Поэтому вектор плотности потока электромагнитной энергии
![]() можно представить как
можно представить как
В случае бегущей гармонической электромагнитной волны (16) плотность энергии, согласно (21), равна

Интенсивность ![]() такой волны равна, по определению, среднему значению плотности потока энергии:
такой волны равна, по определению, среднему значению плотности потока энергии:
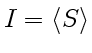 . Принимая во внимание, что при усреднении (24) среднее значение квадрата косинуса равно
. Принимая во внимание, что при усреднении (24) среднее значение квадрата косинуса равно
![]() , получим
, получим
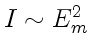 .
.
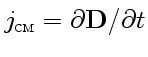 , где
, где
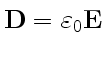 . Пусть
. Пусть
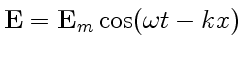 , тогда амплитудное значение плотности тока смещения
, тогда амплитудное значение плотности тока смещения
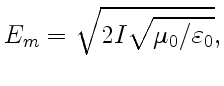
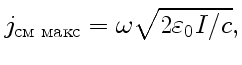
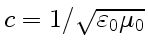 .
.
В стоячей электромагнитной волне энергия переходит из чисто электрической, имеющей максимумы в пучностях
![]() , в магнитную с максимумами в пучностях вектора
, в магнитную с максимумами в пучностях вектора
![]() , т. е. смещенным в пространстве на
, т. е. смещенным в пространстве на ![]() . Это аналогично поведению гармонического осциллятора, например математического маятника, где энергия переходит из чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот.
. Это аналогично поведению гармонического осциллятора, например математического маятника, где энергия переходит из чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот.
Отметим, что если волна представляет собой наложение двух бегущих волн со взаимно перпендикулярными плоскостями поляризации (направлением колебаний вектора
![]() ), то ее интенсивность независимо от особенностей этих волн будет равна сумме интенсивностей складываемых волн. Действительно,
), то ее интенсивность независимо от особенностей этих волн будет равна сумме интенсивностей складываемых волн. Действительно,
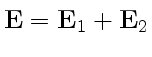 , а интенсивность
, а интенсивность
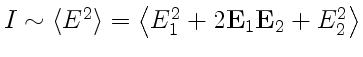 . Поскольку
. Поскольку
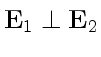 , скалярное произведение
, скалярное произведение
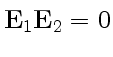 , и мы имеем
, и мы имеем ![]() .
.