Далее: Плоская электромагнитная
Вверх: Электромагнитные волны
Назад: Электромагнитные волны
Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов. При этом изменение его состояния (возмущение поля) обязательно имеет волновой характер. Поля такого рода называютэлектромагнитными волнами. В вакууме эти волны распространяются со скоростью, равной скорости света 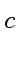 .
.
Рассмотрим однородную нейтральную непроводящую среду с проницаемостями
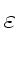 и
и 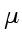 , где
, где
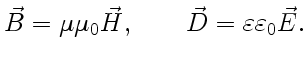 |
(1) |
Поскольку в данном случае плотности зарядов и токов равны нулю (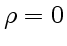 и
и 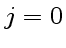 ), уравнения Максвелла будут иметь вид:
), уравнения Максвелла будут иметь вид:
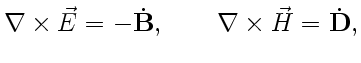 |
(2) |
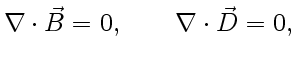 |
(3) |
где уравнения (2) выражают роторы 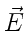 и
и 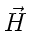 , а уравнения (3) — дивергенции
, а уравнения (3) — дивергенции 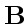 и
и 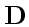 . Точка над векторами
. Точка над векторами
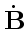 и
и
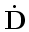 означает частную производную этих величин по времени.
означает частную производную этих величин по времени.
Поскольку любые волновые процессы должны подчиняться волновому уравнению, связывающему вторые производные по времени и координатам, попытаемся получить его с помощью уравнений Максвелла. Для этого продифференцируем второе уравнение из (2) по времени и затем используем первое уравнение:
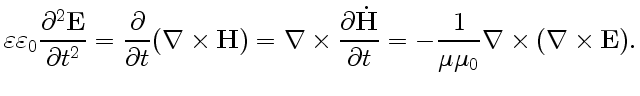 |
(4) |
Двойное векторное произведение в правой части, согласно правилу
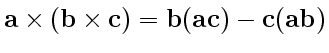 , — "бац минус цаб", можно записать так:
, — "бац минус цаб", можно записать так:
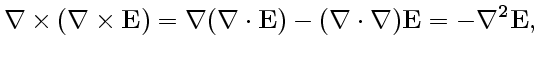 |
(5) |
так как
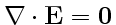 . Подставив (5) в (4), мы приходим к волновому уравнению для
. Подставив (5) в (4), мы приходим к волновому уравнению для  . Аналогично можно получить волновое уравнение и для вектора
. Аналогично можно получить волновое уравнение и для вектора 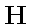 .
.
Таким образом, мы приходим в результате к идентичным волновым уравнениям для векторов  и
и 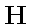 :
:
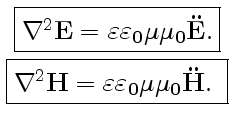 |
(6) |
Здесь коэффициент перед второй производной по времени есть величина, обратная квадрату скорости 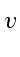 распространения волны,
распространения волны,
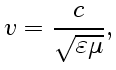 |
(7) |
где c - скорость распространения электромагнитной волны в вакууме:
 |
(8) |
Оказалось, что
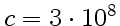 м/с, т. е. совпадает со скоростью света в вакууме. Это и дало основание Максвеллу предположить задолго до экспериментального подтверждения, что свет представляет собой электромагнитные волны.
м/с, т. е. совпадает со скоростью света в вакууме. Это и дало основание Максвеллу предположить задолго до экспериментального подтверждения, что свет представляет собой электромагнитные волны.
Далее: Плоская электромагнитная
Вверх: Электромагнитные волны
Назад: Электромагнитные волны
Отдел образовательных информационных технологий ЯГПУ
08.02.2014
![]() .
.
![]() и
и ![]() , где
, где
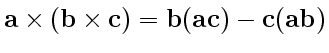 , — "бац минус цаб", можно записать так:
, — "бац минус цаб", можно записать так:
![]() и
и ![]() :
: