Перепишем уравнения Максвелла (1) и (2) в форме более удобной для дальнейшего анализа, имея в виду, что роторы
![]() и
и
![]() можно представить в виде определителей (как векторное произведение двух векторов):
можно представить в виде определителей (как векторное произведение двух векторов):
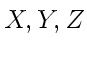 .
.
Установим основные свойства электромагнитной волны на примере плоской волны. Направим ось ![]() перпендикулярно волновым поверхностям. При этом
перпендикулярно волновым поверхностям. При этом
![]() и
и
![]() , а значит и их проекции на оси
, а значит и их проекции на оси ![]() и
и ![]() , не будут зависеть от координат
, не будут зависеть от координат ![]() и
и ![]() , т. е. соответствующие производные по
, т. е. соответствующие производные по ![]() и
и ![]() , будут равны нулю. Пэтому уравнения (9) и (10) упрощаются (останутся только произвоные по
, будут равны нулю. Пэтому уравнения (9) и (10) упрощаются (останутся только произвоные по ![]() ) и принимают вид:
) и принимают вид:
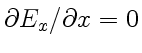 , и
, и
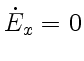 следует, что
следует, что
Кроме того, оказывается, векторы ![]() и
и ![]() в электромагнитной волне взаимно ортогональны. Чтобы убедиться в этом, объединим средние уравнения (11), содержащие, например,
в электромагнитной волне взаимно ортогональны. Чтобы убедиться в этом, объединим средние уравнения (11), содержащие, например, ![]() и
и ![]() , в пару:
, в пару:
 .
.
Связь мгновенных значений E и H. В нашем случае, когда плоская волна распространяется вдоль оси ![]() , например, в ее положительном направлении,
, например, в ее положительном направлении,
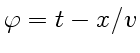 , найдем производные
, найдем производные 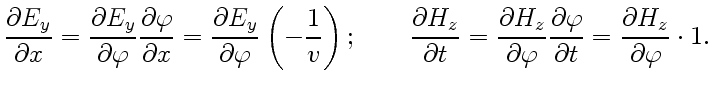
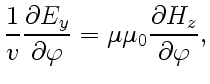
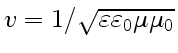 ,
,
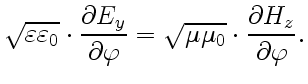
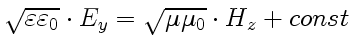 , где произвольная константа обусловлена наличием постоянного электрического и магнитного полей. Нас интересует только переменное поле, поэтому
, где произвольная константа обусловлена наличием постоянного электрического и магнитного полей. Нас интересует только переменное поле, поэтому
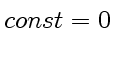 , в результате мы получим:
, в результате мы получим:
Это выражение означает, что
![]() и
и
![]() не только взаимно ортогональны, но и составляют правовинтовую систему с направлением распространения: мы ведь рассмотрели случай, когда волна распространяется в положительном направлении оси
не только взаимно ортогональны, но и составляют правовинтовую систему с направлением распространения: мы ведь рассмотрели случай, когда волна распространяется в положительном направлении оси ![]() (рис.1).
(рис.1).
Кроме того,
![]() и
и
![]() , согласно (14), изменяются при этом синфазно:
, согласно (14), изменяются при этом синфазно: ![]() и
и ![]() одинаковы в каждый момент по знаку, одновременно обращаются в нуль и одновременно достигают максимума, что и показано на рис.2 — мгновенная картина в некоторый момент.
одинаковы в каждый момент по знаку, одновременно обращаются в нуль и одновременно достигают максимума, что и показано на рис.2 — мгновенная картина в некоторый момент.
Заметим, что если бы мы рассмотрели волну, распространяющуюся в отрицательном направлении оси ![]() , то
, то
![]() и
и ![]() изменялись бы в противофазе
(
изменялись бы в противофазе
(
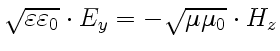 ). Однако по-прежнему оба вектора,
). Однако по-прежнему оба вектора,
![]() и
и
![]() , составляли бы правовинтовую систему с направлением распространения. Это же относится и к случаю, когда
, составляли бы правовинтовую систему с направлением распространения. Это же относится и к случаю, когда
![]() направлен вдоль оси
направлен вдоль оси ![]() , а
, а
![]() — вдоль оси
— вдоль оси ![]() , т. е. их проекции
, т. е. их проекции
![]() и
и ![]() .
.
Выяснив эти детали, индексы ![]() и
и ![]() у проекций векторов
у проекций векторов
![]() и
и
![]() можно не писать (как это обычно и делают). Поэтому уравнение, например, плоской бегущей гармонической волны — она представляет особый интерес — записывают так:
можно не писать (как это обычно и делают). Поэтому уравнение, например, плоской бегущей гармонической волны — она представляет особый интерес — записывают так:
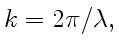
Заметим, что когда говорят, что плоская волна распространяется,например, в положительном направлении оси ![]() , то это означает, что с этим направлением совпадает ее волновой вектор
, то это означает, что с этим направлением совпадает ее волновой вектор
![]() или, другими словами, ее волновые поверхности ортогональны оси
или, другими словами, ее волновые поверхности ортогональны оси ![]() . Но при этом колебания распространяются очевидно и в других направлениях.
. Но при этом колебания распространяются очевидно и в других направлениях.
Изобразив рисунок, аналогичный рис. 1, найдем, что искомая скорость
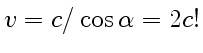 Полученный результат не противоречит теории относительности: фазовая скорость может быть любой, в отличие от скорости сигнала, которая не может быть больше
Полученный результат не противоречит теории относительности: фазовая скорость может быть любой, в отличие от скорости сигнала, которая не может быть больше ![]() — скорости света в вакууме.
— скорости света в вакууме.
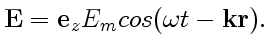
![$ [\strut\mathbf{kE}]$](img76.gif) , направление которого совпадает с ортом
, направление которого совпадает с ортом
![$ [{\bf n}_k{\bf e}_z]$](img77.gif) , где орт
, где орт
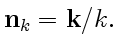 Остается найти модуль вектора
Остается найти модуль вектора
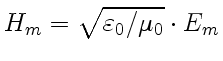 . В результате получим:
. В результате получим:
![$\displaystyle {\bf H}=[{\bf n}_k {\bf e}_z]\sqrt{\varepsilon_0/\mu_0} \cdot E_m.
$](img80.gif)