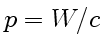 , где
, где
Перенос энергии электромагнитной волной сопровождается и переносом импульса. Согласно теории относительности, импульс объекта с нулевой массой покоя, движущегося со скоростью света, 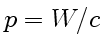 , где
, где ![]() — его энергия (это по — существу верно и для электромагнитной волны как потоку фотонов). Поскольку в случае электромагнитной волны масса покоя "lобъекта" равна нулю, связь между энергией и импульсом будет такой же:
— его энергия (это по — существу верно и для электромагнитной волны как потоку фотонов). Поскольку в случае электромагнитной волны масса покоя "lобъекта" равна нулю, связь между энергией и импульсом будет такой же:
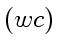 , которая в свою очередь равна модулю вектора Пойнтинга. Таким образом, в векторном виде
, которая в свою очередь равна модулю вектора Пойнтинга. Таким образом, в векторном виде
Если падающая нормально на поверхность некоторого тела электромагнитная волна полностью поглощается этим телом, то единице площади поверхности тела сообщается за промежуток времени ![]() импульс, заключенный в цилиндре с площадью сечения, равной единице, и высотой
импульс, заключенный в цилиндре с площадью сечения, равной единице, и высотой ![]() , т. е.
, т. е.
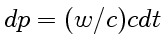 . Но импульс, сообщаемый единице поверхности в единицу времени,
. Но импульс, сообщаемый единице поверхности в единицу времени, 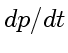 , равен давлению
, равен давлению ![]() на поверхность тела. Поэтому для поглощающей поверхности давление
на поверхность тела. Поэтому для поглощающей поверхности давление ![]() ,
,
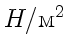 . В случае гармонической волны эта величина пульсирует с достаточно большой частотой, и практически представляет интерес лишь ее среднее значение по времени:
. В случае гармонической волны эта величина пульсирует с достаточно большой частотой, и практически представляет интерес лишь ее среднее значение по времени:
Рассмотрим более детально механизм передачи импульса телу, т. е. как возникает давление. Электрическое поле волны возбуждает в теле ток плотности
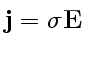 , а магнитное волны будет действовать на
, а магнитное волны будет действовать на
![]() в соответствии с законом Ампера — с силой, объемная плотность которой равна
в соответствии с законом Ампера — с силой, объемная плотность которой равна
Надо иметь в виду, что электромагнитная волна оказывает давление не только внутри вещества (при условии, что удельная проводимость
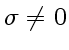 ), но и при отражении от поверхности так что
), но и при отражении от поверхности так что
Давление, вычисленное по формуле (28), оказывается в обычных условиях очень малым. Например, солнечный свет оказывает давление порядка ![]() Па (атмосферное давление
Па (атмосферное давление
![]() Па). Измерить такое давление экспериментально очень трудно. Впервые это удалось П. Н. Лебедеву (в 1900 г.). Его измерения дали значение, согласующееся с теорией с точностью до 20%. Позднее эти измерения повторил Герлах (в 1923 г.), достигнув точности до 2%.
Па). Измерить такое давление экспериментально очень трудно. Впервые это удалось П. Н. Лебедеву (в 1900 г.). Его измерения дали значение, согласующееся с теорией с точностью до 20%. Позднее эти измерения повторил Герлах (в 1923 г.), достигнув точности до 2%.
Тот факт, что электромагнитное поле обладает импульсом, предписывает при составлении баланса импульсов частиц учитывать и импульс электромагнитного поля. Только при этом с законом сохранения импульса будет все в порядке.