Рассмотрим идеализированный
случай, когда источники ![]() и
и ![]() строго монохроматические. В
интересующую нас точку экрана колебания от этих источников будут
приходить практически с одинаковой амплитудой,
строго монохроматические. В
интересующую нас точку экрана колебания от этих источников будут
приходить практически с одинаковой амплитудой,
![]() .
Тогда, согласно (1),
.
Тогда, согласно (1),
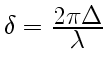 . В
нашем случае (см. рис. 3)
. В
нашем случае (см. рис. 3)
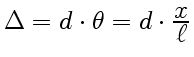 . Следовательно,
. Следовательно,
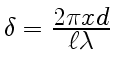 . Имея
в виду, что интенсивность
. Имея
в виду, что интенсивность 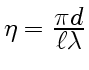 ,
,
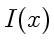 несколько
отличается, естественно, от реального, которому соответствует
рис. 3.
несколько
отличается, естественно, от реального, которому соответствует
рис. 3.