![$\displaystyle \left.\begin{array}{rcl} \vec E=\vec E_p+\vec E_s, [3pt] \vec E...
... E'_p+\vec E'_s, [3pt] \vec E''=\vec E''_p+\vec E''_s, \end{array} \right\}$](img77.gif) |
(26) |
Определим теперь распределение интенсивности света между отраженными и преломленными световыми волнами. С этой целью удобно разложить вектор напряженности электрического поля (световой вектор) у всех трех волн на два взаимно перпендикулярных вектора — один в плоскости падения, другой — перпендикулярно этой плоскости:
Как следует из (рис.5),
Чтобы определить отношение амплитуд падающей и отраженной волн,
напишем граничные условия (13) и (14):
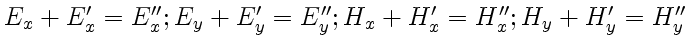 .
Следовательно,
.
Следовательно,
Эти формулы называются формулами Френеля. Впервые они были выведены Френелем в 1823г. на основе его теории, согласно которой свет представляет собой колебание упругой среды — эфира. Свободный от противоречий вывод формул Френеля, как мы видели выше, основан на электромагнитной теории света, где световые колебания отождествляются с колебаниями электрического вектора. Если обратить внимание на тот факт, что действия света в основном обусловлены электрическим (световым) вектором, то подобное отождествление можно считать законным.
Как следует из (29), при
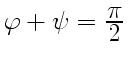 , т. е. при
, т. е. при
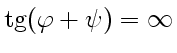 ,
, 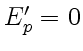 ,
, 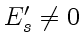 . Это означает,
что если лучи, отраженный и преломленный, взаимно перпендикулярны,
то в отраженной волне колебание электрического вектора происходит
только в одном направлении — в направлении, перпендикулярном
плоскости падения. Такой луч, как мы уже знаем называется линейно
— или плоскополяризованным. Угол падения естественного света,
при котором отраженный луч плоскополяризован, называется углом
Брюстера.
. Это означает,
что если лучи, отраженный и преломленный, взаимно перпендикулярны,
то в отраженной волне колебание электрического вектора происходит
только в одном направлении — в направлении, перпендикулярном
плоскости падения. Такой луч, как мы уже знаем называется линейно
— или плоскополяризованным. Угол падения естественного света,
при котором отраженный луч плоскополяризован, называется углом
Брюстера.