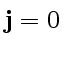 ) и (
) и (
Запишем первое волновое уравнение системы (6) для волны распространяющейся в вакууме при (
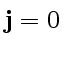 ) и (
) и (![]() ) в виде
) в виде
где ![]() — скорость света в вакууме, определяемая выражением (8).
Большую роль в физике играет волновое уравнение. Для скалярной функции
— скорость света в вакууме, определяемая выражением (8).
Большую роль в физике играет волновое уравнение. Для скалярной функции
![]() оно имеет вид
оно имеет вид
Найдем общее решение этого уравнения для случая, когда
![]() зависит только от одной из декартовых координат, например
зависит только от одной из декартовых координат, например ![]() , т. е.
, т. е.
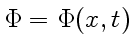 .
.