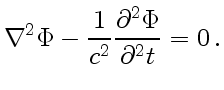 |
(50) |
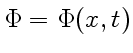 . Это означает, что
. Это означает, что
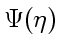 . После этого уравнение (58) принимает вид
. После этого уравнение (58) принимает вид
Интегрируя (59) по ![]() , получаем
, получаем
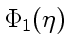 — первообразная функция в интеграле от
— первообразная функция в интеграле от
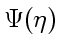 по
по 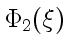 — постоянная интегрирования. Как видно по ходу решения, функции
— постоянная интегрирования. Как видно по ходу решения, функции Выясним физический смысл этого решения. Сначала проанализируем решение
График ![]() как функции от
как функции от ![]() в моменты времени
в моменты времени ![]() и
и
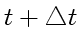 изображен на рис. 9.
Видно, что значение аргумента функции в точке
изображен на рис. 9.
Видно, что значение аргумента функции в точке ![]() в момент
в момент ![]() совпадает со значением аргумента функции в точке
совпадает со значением аргумента функции в точке
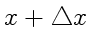 в момент
в момент
 , если
, если
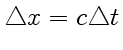 , поскольку
, поскольку
Поэтому график функции для
 получается из графика для
получается из графика для ![]() смещением всех точек кривой в направлении положительных значений оси
смещением всех точек кривой в направлении положительных значений оси ![]() на
на
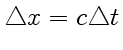 . Следовательно, скорость волны равна
. Следовательно, скорость волны равна
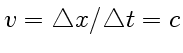 . Функция
. Функция
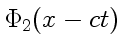 описывает волну произвольной формы, движущуюся со скоростью
описывает волну произвольной формы, движущуюся со скоростью ![]() в направлении положительных значений оси
в направлении положительных значений оси ![]() . В процессе движения
значение
. В процессе движения
значение ![]() в каждой точке волны и форма волны не изменяются.
в каждой точке волны и форма волны не изменяются.
Физический смысл ![]() , т. е. решения
, т. е. решения
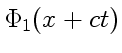 описывает волну произвольной формы, движущуюся со скоростью
описывает волну произвольной формы, движущуюся со скоростью
Волна, описываемая формулой (62), является суперпозицией двух волн, движущихся в противоположных направлениях. В этом случае уже нельзя говорить о скорости или направлении волны. В простейшем случае получается стоячая волна, а в общем случае — сложное электромагнитное поле, которое требует специального изучения.
Значение функции
![]() для фиксированных
для фиксированных ![]() и
и ![]() является постоянным на плоскости, перпендикулярной оси
является постоянным на плоскости, перпендикулярной оси ![]() . Поэтому такие волны называются плоскими.
. Поэтому такие волны называются плоскими.