Приложения
3. Ранговая корреляция по Спирмену
В тех случаях, когда необходимо установить возможную функциональную связь между двумя изучаемыми параметрами, используют метод называемый ранговой корреляцией. Например, группа испытуемых последовательно выполняет тестовые задания в беге на 30м и тройном прыжке с места. Требуется определить влияет ли уровень развития быстроты на результат в прыжке.
В поисках ответа на поставленный вопрос сравнивают места (ранги), которые занимает каждый участник в каждом из обоих видов.
Иногда даже визуальное сопоставление рангов говорит в пользу функциональной взаимозависимости исследуемых показателей. Однако более обоснованное заключение можно получить лишь с помощью приемов статистической обработки материала. Ее технологии достаточно проста и она изложена в табл. 4
Таблица 4
Определение коррелятивной зависимости между результатами в беге на 30м и тройным прыжком с места
|
№ п\п |
Испытуемые (n = 10) |
Тройной с места (см) |
Ранги |
Бег 30 м (с) |
Ранги |
Разность рангов di |
Квадраты разности рангов di2 |
|
1 |
А. |
744 |
5 |
4,2 |
5,5 |
0,5 |
0,25 |
|
2 |
Б |
613 |
10 |
4,5 |
10 |
0 |
0 |
|
3 |
В |
737 |
6,5 |
4,3 |
7,5 |
1 |
1 |
|
4 |
Г |
623 |
8 |
4,3 |
7,5 |
1,5 |
2,25 |
|
5 |
Д |
618 |
9 |
4,4 |
9 |
0 |
0 |
|
6 |
Е |
745 |
3,5 |
4,0 |
2,5 |
1 |
1 |
|
7 |
Ж |
737 |
6,5 |
4,2 |
5,5 |
1 |
1 |
|
8 |
З |
750 |
2 |
4,0 |
2,5 |
1,5 |
2,25 |
|
9 |
И |
745 |
3,5 |
4,1 |
4 |
0,5 |
0,25 |
|
10 |
К |
760 |
1 |
3,9 |
1 |
0 |
0 |
Сначала в таблицу вносятся результаты испытуемых в тройном прыжке и определяются ранги (места) каждого участника. Если два или более результата одинаковы, то им присваивается одинаковый ранг, составляющий среднеарифметическое значение нормального ряда чисел (см. § 2). Далее в очередную графу вносятся результаты в беге, которые ранжируются по уже известной схеме.
Сопоставляя парные ранги, находят их арифметическую разность (di), после чего каждая из найденных разностей возводится в квадрат (di2). Затем определяется сумма этих квадратов разностей (∑di2). Далее с помощью формулы находится коэффициент корреляции, (число 6 в формуле – постоянное).
Сумма квадратов разностей в нашем случае составила 4,0. Подставляя все значения в формулу, находим, что r = 0,98
Из таблицы 5 находим, что при n = 10 значимый уровень корреляции составляет менее 0,001, что говорит об очень высокой функциональной взаимосвязи исследуемых показателей.
Таблица 5
Минимальные значения коэффициентов нормальной корреляции, при которых связь между двумя рядами наблюдений можно считать значимой с уровнем надежности Р; n – число пар сравниваемых наблюдений
|
Р n |
0,05 |
0,01 |
0,005 |
|
5 |
0,669 |
0,833 |
0,875 |
|
7 |
0,582 |
0,750 |
0,798 |
|
10 |
0,497 |
0,658 |
0,708 |
|
12 |
0,457 |
0,612 |
0,661 |
|
15 |
0,412 |
0,558 |
0,606 |
|
18 |
0,378 |
0,516 |
0,561 |
|
20 |
0,360 |
0,492 |
0,537 |
|
25 |
0,323 |
0,445 |
0,487 |
|
30 |
0,296 |
0,409 |
0,449 |
В табличном редакторе Excel коэффициент корреляции находим, вычислив ранги, как было показано выше.

Рис. 4. Вставка формулы в «строку формул»
Затем в следующем столбце (К) найдем разности рангов с последующим возведением в квадрат (столбец L), для чего в «строку формул» внесем нужные формулы: =H3-J3 и = Кˆ2. В ячейке L14 находим сумму квадратов разностей рангов (СУММ (L3:L12)) (рис. 4).
Далее на основании полученных цифровых данных производим расчет коэффициента корреляции. Для этого в «строку формул» вносим формулу =1-(6*L14)/(10*(10ˆ2-1)) (рис. 5).
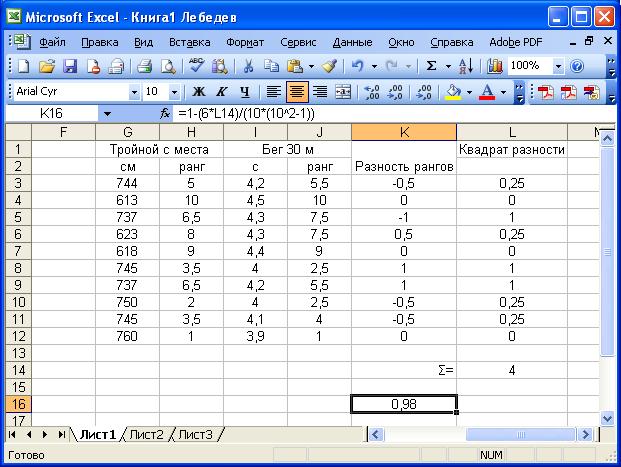
Рис. 5. Расчет коэффициента корреляции
Кроме рассмотренных непараметрических существуют параметрические методы математической статистики. К ним относятся критерий Т Крамера – Уэлча, t-критерий Стьюдента, корреляция Пирсона. Они более точны, хотя и более трудоемки, однако сфера их применения ограничена выборками с относительно небольшими отклонениями параметров от их средней величины.
Таким образом, достоверность сдвигов с применением этих методик может определяться как в «ручном» варианте, так и с помощью специальных компьютерных программ.