1) эфир совершенно не возмущается движущими телами; 2) эфир увлекается движущимися телами частично, приобретая скорость, равную
До сих пор мы предполагали, что источники, приемники и другие тела, относительно которых рассматривалось распространение света, неподвижны. Естественно заинтересоваться вопросом, как скажется на распространении света движение источника световых волн. При этом возникает необходимость указать, относительно чего происходит движение. В §1.11 (И.В.Савельев ``Курс общей физики'' кн.1) мы выяснили, что движение источника или приемника звуковых волн относительно среды, в которой эти волны распространяются, оказывает илияние на протекающие акустические явления (эффект Доплера) и, следовательно, может быть обнаружено.
Первоначально волновая теория рассматривала свет как упругие волны, распространяющиеся в некой гипотетической среде, получившей название мирового эфира. После создания теории Максвелла на смену упругому эфиру пришел эфир — носитель электромагнитных волн и полей. Под этим эфиром подразумевалась особая среда, наполняющая, как и ее предшественник, упругий эфир, все мировое пространство и пронизывающая все тела. Раз эфир представлял собой некую среду, можно было рассчитывать обнаружить движение тел, например источников или приемников света, по отношению к этой среде. В частности, следовало ожидать существования «эфирного ветра», обдувающего Землю при ее движении вокруг Солнца.
В механике был установлен принцип относительности Галилея, согласно которому все инерциальные системы отсчета являются в механическом отношении равноправными. Обнаружение эфира сделало бы возможным выделение (с помощью оптических явлений) особенной (связанный с эфиром), преимущественной, абсолютной системы отсчета. Тогда движение остальных систем можно было бы рассматривать по отношению к этой абсолютной системе.
Таким образом, выяснение вопроса о взаимодействии мирового эфира с
движущимися телами играло принципиальную роль. Можно было
допустить три возможности:
1) эфир совершенно не
возмущается движущими телами; 2) эфир увлекается движущимися
телами частично, приобретая скорость, равную
![]() , где
, где ![]() —
скорость тела относительно абсолютной системы отсчета,
—
скорость тела относительно абсолютной системы отсчета, ![]() —
коэффициент увлечения, меньший единицы; 3) эфир полностью
увлекается движущимися телами, например Землей, подобно тому, как
тело при своем движении увлекает прилежащие к его поверхности слои
газа. Однако последняя возможность опровергается существованием
явления аберрации света. В предыдущем параграфе мы выяснили, что
изменение видимого положения звезд может быть объяснено движением
телескопа относительно системы отсчета (среды), в которой
распространяется световая волна.
—
коэффициент увлечения, меньший единицы; 3) эфир полностью
увлекается движущимися телами, например Землей, подобно тому, как
тело при своем движении увлекает прилежащие к его поверхности слои
газа. Однако последняя возможность опровергается существованием
явления аберрации света. В предыдущем параграфе мы выяснили, что
изменение видимого положения звезд может быть объяснено движением
телескопа относительно системы отсчета (среды), в которой
распространяется световая волна.
Для выяснения вопроса о том, увлекается ли эфир движущимися телами
телами, Физо осуществил в 1851г. следующий опыт. Параллельный
пучок света от источника ![]() разделялся посеребренной
полупрозрачной пластинкой
разделялся посеребренной
полупрозрачной пластинкой ![]() на два пучка, обозначенных цифрами
на два пучка, обозначенных цифрами
![]() и
и ![]() (рис.24).
(рис.24).
За счет отражения от зеркал ![]() ,
, ![]() и
и ![]() пучки, пройдя в
общей сложности одинаковый путь
пучки, пройдя в
общей сложности одинаковый путь ![]() , снова попадали на пластинку
, снова попадали на пластинку
![]() . Пучок
. Пучок ![]() частично проходил через
частично проходил через ![]() , пучок
, пучок ![]() частично
отражался, в результате чего возникали два когерентных пучка
частично
отражался, в результате чего возникали два когерентных пучка ![]() и
и ![]() , которые давали в фокальной плоскости зрительной трубы
интерференционную картину в виде полос. На пути пучков
, которые давали в фокальной плоскости зрительной трубы
интерференционную картину в виде полос. На пути пучков ![]() и
и ![]() были установлены две трубы, по которым могла пропускаться вода со
скоростью
были установлены две трубы, по которым могла пропускаться вода со
скоростью ![]() и в направлениях, указанных стрелками. Луч
и в направлениях, указанных стрелками. Луч ![]() распространялся в обеих трубах навстречу току воды, луч
распространялся в обеих трубах навстречу току воды, луч ![]() — по
течению.
— по
течению.
При неподвижной воде пучки ![]() и
и ![]() проходят путь
проходят путь ![]() за
одинаковое время. Если вода при своем движении хотя бы частично
увлекает эфир, то при включении тока воды луч
за
одинаковое время. Если вода при своем движении хотя бы частично
увлекает эфир, то при включении тока воды луч ![]() , который
распространяется против течения, затратит на прохождение пути
, который
распространяется против течения, затратит на прохождение пути ![]() большее время, чем луч
большее время, чем луч ![]() , распространяющийся по течению. В
результате между лучами возникнет некоторая разность хода, и
интерференционная картина сместится.
, распространяющийся по течению. В
результате между лучами возникнет некоторая разность хода, и
интерференционная картина сместится.
При неподвижной воде пучки ![]() и
и ![]() проходят путь
проходят путь ![]() за
одинаковое время. Если вода при своем движении хотя бы частично
увлекает эфир, то при включении тока воды луч
за
одинаковое время. Если вода при своем движении хотя бы частично
увлекает эфир, то при включении тока воды луч ![]() , который
распространяется против течения, затратит на прохождение пути
, который
распространяется против течения, затратит на прохождение пути ![]() большее время, чем луч
большее время, чем луч ![]() , распространяющийся по течению. В
результате между лучами возникнет некоторая разность хода, и
интерференционная картина сместится.
, распространяющийся по течению. В
результате между лучами возникнет некоторая разность хода, и
интерференционная картина сместится.
Интересующая нас разность хода возникает лишь на пути лучей,
пролегающем в воде. Этот путь имеет длину ![]() . Обозначим
скорость света относительно эфира в воде буквой
. Обозначим
скорость света относительно эфира в воде буквой ![]() . Когда эфир не
увлекается водой, скорость света относительно установки будет
совпадать с
. Когда эфир не
увлекается водой, скорость света относительно установки будет
совпадать с ![]() . Предположим, что вода при своем движении частично
увлекает эфир, сообщая ему относительно установки скорость
. Предположим, что вода при своем движении частично
увлекает эфир, сообщая ему относительно установки скорость
![]() (
(![]() — скорость воды,
— скорость воды, ![]() — коэффициент увлечения). Тогда
скорость света относительно установки будет равна
— коэффициент увлечения). Тогда
скорость света относительно установки будет равна
![]() для луча 1 и
для луча 1 и
![]() для луча
для луча ![]() . Луч
. Луч ![]() пройдет путь
пройдет путь
![]() за время
за время
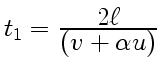 , луч
, луч ![]() — за время
— за время
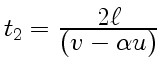 . Из формулы
. Из формулы
 вытекает,
что оптическая длина пути
вытекает,
что оптическая длина пути ![]() , на прохождение которой
затрачивается время
, на прохождение которой
затрачивается время ![]() , равна
, равна ![]() . Следовательно, разность хода
лучей
. Следовательно, разность хода
лучей ![]() и
и ![]() равна
равна
 . Разделив
. Разделив
![]() на
на ![]() , получим число полос, на которое
сместится интерференционная картина при включении тока воды:
, получим число полос, на которое
сместится интерференционная картина при включении тока воды:
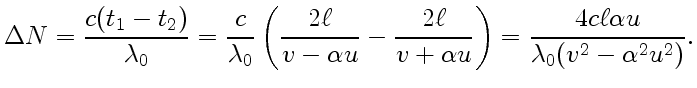
Физо обнаружил, что интерференционные полосы действительно смещаются. Соответствующее смещению значение коэффициента увлечения оказалось равным
Легко убедиться в том, что результат опыта Физо объясняется
релятивистским законом сложения скоростей. Согласно формуле (6.33)
И.В.Савельев ``Курс общей физики'' кн.1 скорости ![]() и
и
![]() некоторого тела в системах
некоторого тела в системах ![]() и
и ![]() связаны соотношением
связаны соотношением
Свяжем с прибором Физо систему отсчета ![]() , а с движущейся водой —
систему
, а с движущейся водой —
систему ![]() . Тогда роль
. Тогда роль ![]() будет играть скорость течения воды
будет играть скорость течения воды
![]() , роль
, роль ![]() — скорость света относительно воды, равная
— скорость света относительно воды, равная
![]() , и, наконец, роль
, и, наконец, роль ![]() —
скорость света относительно прибора
—
скорость света относительно прибора
![]() .
Подстановка этих значений в формулу (42) дает
.
Подстановка этих значений в формулу (42) дает
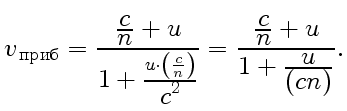
Согласно классическим представлениям скорость света относительно
прибора
![]() равна сумме скорости света
относительно эфира, т. е.
равна сумме скорости света
относительно эфира, т. е.
![]() , и
скорости эфира относительно прибора, т. е.
, и
скорости эфира относительно прибора, т. е.
![]() :
:
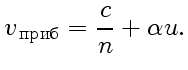
Следует иметь в виду, что одинакова во всех системах отсчета лишь
скорость света в вакууме. Скорость света в веществе различна в
разных системах отсчета. Значение
![]() она имеет в системе отсчета, связанной со
средой, в которой происходит распространение света.
она имеет в системе отсчета, связанной со
средой, в которой происходит распространение света.