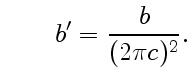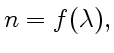 |
(15) |
Дисперсия света — это явления, обусловленные зависимостью показателя преломления вещества от длины волны (или частоты):
Производную
![]() ,
называют дисперсией вещества. Для прозрачных бесцветных
веществ график зависимости
,
называют дисперсией вещества. Для прозрачных бесцветных
веществ график зависимости
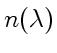 в видимой части спектра
имеет вид, показанный на рис.10.
в видимой части спектра
имеет вид, показанный на рис.10.
Интервал длин волн, в котором
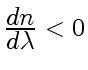 (как на рисунке), соответствует нормальной
дисперсии. Те же интервалы длин волн, где дисперсия вещества
(как на рисунке), соответствует нормальной
дисперсии. Те же интервалы длин волн, где дисперсия вещества
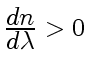 , соответствуют
аномальной дисперсии. На рис.11 показан
график зависимости
, соответствуют
аномальной дисперсии. На рис.11 показан
график зависимости
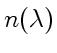 с участками нормальной и
аномальной дисперсии. Заметим, что область аномальной дисперсии
совпадает с полосой поглощения
с участками нормальной и
аномальной дисперсии. Заметим, что область аномальной дисперсии
совпадает с полосой поглощения
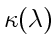 .
.
Все вещества в той или иной степени являются диспергирующими. Вакуум, как показали тщательные исследования, дисперсией не обладает.
Аналитический вид зависимости
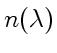 в области нормальной
дисперсии для не слишком больших интервалов длин волн может быть
представлен приближенной формулой
в области нормальной
дисперсии для не слишком больших интервалов длин волн может быть
представлен приближенной формулой
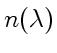 . Изобразим соответствующие графики зависимостей
. Изобразим соответствующие графики зависимостей 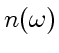 , где
, где
Поскольку
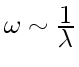 ,
легко проверить, что графики
,
легко проверить, что графики 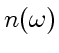 , соответствующие
указанным рисункам, таковы, как показано на
рис.12 и 13. Причем, в случае
графика, приведенного на рис.12, закон дисперсии
в соответствии с формулой (16) принимает вид
, соответствующие
указанным рисункам, таковы, как показано на
рис.12 и 13. Причем, в случае
графика, приведенного на рис.12, закон дисперсии
в соответствии с формулой (16) принимает вид
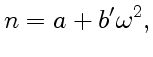 где постоянная
где постоянная