Поместим между поляризаторами2 ![]() и
и ![]() пластинку из одноосного кристалла, вырезанную параллельно
оптической оси
пластинку из одноосного кристалла, вырезанную параллельно
оптической оси ![]() (рис.4). Из поляризатора
(рис.4). Из поляризатора ![]() выйдет плоскополяризованный свет интенсивности
выйдет плоскополяризованный свет интенсивности ![]() . Пройдя через
пластинку, свет станет в общем случае эллиптически поляризованным.
По выходе из поляризатора
. Пройдя через
пластинку, свет станет в общем случае эллиптически поляризованным.
По выходе из поляризатора ![]() свет снова будет
плоскополяризованным.
свет снова будет
плоскополяризованным.
Его интенсивность ![]() зависит от взаимной ориентации плоскостей
поляризаторов
зависит от взаимной ориентации плоскостей
поляризаторов ![]() и
и ![]() и оптической оси пластинки, а также от
разности фаз
и оптической оси пластинки, а также от
разности фаз ![]() , приобретаемой обыкновенным и необыкновенным
лучами при прохождении через пластинку.
, приобретаемой обыкновенным и необыкновенным
лучами при прохождении через пластинку.
Предположим, что угол ![]() между плоскостью поляризатора
между плоскостью поляризатора ![]() и осью пластинки
и осью пластинки ![]() равен
равен
![]() .
Рассмотрим два частных случая: поляризаторы параллельны
(рис.5а) и поляризаторы скрещены
(рис.5б).
.
Рассмотрим два частных случая: поляризаторы параллельны
(рис.5а) и поляризаторы скрещены
(рис.5б).
Световое колебание, вышедшее из поляризатора ![]() , изобразится
вектором
, изобразится
вектором
![]() , лежащим в плоскости
, лежащим в плоскости ![]() . При входе в
пластинку колебание
. При входе в
пластинку колебание
![]() возбудит два колебания —
перпендикулярное к оптической оси колебание
возбудит два колебания —
перпендикулярное к оптической оси колебание
![]() (обыкновенный луч) и параллельное оси колебание
(обыкновенный луч) и параллельное оси колебание
![]() (необыкновенный луч). Эти колебания будут когерентными; проходя
через пластинку, они приобретут разность фаз
(необыкновенный луч). Эти колебания будут когерентными; проходя
через пластинку, они приобретут разность фаз ![]() , которая
определяется толщиной пластинки и разностью показателей
преломления обыкновенного и необыкновенного лучей. Амплитуды этих
колебаний одинаковы и равны
, которая
определяется толщиной пластинки и разностью показателей
преломления обыкновенного и необыкновенного лучей. Амплитуды этих
колебаний одинаковы и равны
Через второй поляризатор пройдут составляющие колебаний
![]() и
и
![]() по направлению плоскости
по направлению плоскости ![]() .
Амплитуды этих составляющих в обоих случаях равны амплитудам
(4), умноженным на
.
Амплитуды этих составляющих в обоих случаях равны амплитудам
(4), умноженным на
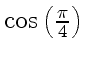 ,
т. е.
,
т. е.
Волны, вышедшие из второго поляризатора, будут интерферировать.
Амплитуда
![]() результирующей волны в случае
параллельных поляризаторов определяется соотношением
результирующей волны в случае
параллельных поляризаторов определяется соотношением
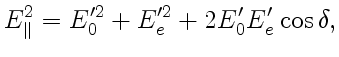
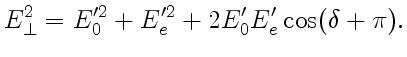
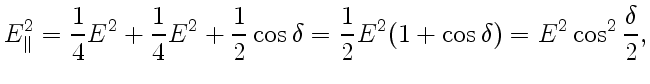
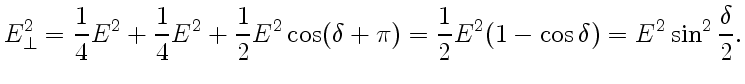
Из формул (6) следует, что интенсивности
![]() и
и
![]() оказываются «дополнительными» — в
сумме они дают интенсивность
оказываются «дополнительными» — в
сумме они дают интенсивность ![]() . В частности, при
. В частности, при
Разность показателей преломления ![]() зависит от длины волны
света
зависит от длины волны
света ![]() . Кроме того,
. Кроме того, ![]() входит непосредственно
в выражение (3) для
входит непосредственно
в выражение (3) для ![]() . Пусть свет, падающий
на поляризатор
. Пусть свет, падающий
на поляризатор ![]() , состоит из излучения двух длин волн
, состоит из излучения двух длин волн
![]() и
и ![]() , таких, что
, таких, что ![]() для
для ![]() удовлетворяет условию (7), а для
удовлетворяет условию (7), а для ![]() —
условию (8). В этом случае при параллельных
поляризаторах через систему, изображенную на
рис.4, пройдет беспрепятственно свет с длиной
волны
—
условию (8). В этом случае при параллельных
поляризаторах через систему, изображенную на
рис.4, пройдет беспрепятственно свет с длиной
волны ![]() и полностью будет задержан свет с длиной волны
и полностью будет задержан свет с длиной волны
![]() . При скрещенных поляризаторах пройдет беспрепятственно
свет с длиной волны
. При скрещенных поляризаторах пройдет беспрепятственно
свет с длиной волны ![]() и полностью будет задержан свет с
длиной волны
и полностью будет задержан свет с
длиной волны ![]() . Следовательно, при одном расположении
поляризаторов окраска прошедшего через систему света будет
соответствовать длине волны
. Следовательно, при одном расположении
поляризаторов окраска прошедшего через систему света будет
соответствовать длине волны ![]() , при другом расположении —
длине волны
, при другом расположении —
длине волны ![]() . Такие две окраски называются дополнительными. При вращении одного из поляризаторов окраска
непрерывно меняется, переходя за каждую четверть оборота от одного
дополнительного цвета к другому. Смена окраски наблюдается и при
. Такие две окраски называются дополнительными. При вращении одного из поляризаторов окраска
непрерывно меняется, переходя за каждую четверть оборота от одного
дополнительного цвета к другому. Смена окраски наблюдается и при
![]() , отличном от
, отличном от
![]() (но
не равном нулю или
(но
не равном нулю или
![]() ), только
цвета оказываются менее насыщенными.
), только
цвета оказываются менее насыщенными.
Разность фаз ![]() зависит от толщины пластинки. Поэтому, если
двоякопреломляющая прозрачная пластинка, помещенная между
поляризаторами, имеет в разных местах неодинаковую толщину, эти
места при наблюдении со стороны поляризатора
зависит от толщины пластинки. Поэтому, если
двоякопреломляющая прозрачная пластинка, помещенная между
поляризаторами, имеет в разных местах неодинаковую толщину, эти
места при наблюдении со стороны поляризатора ![]() будут
представляться окрашенными в различные цвета. При вращении
поляризатора
будут
представляться окрашенными в различные цвета. При вращении
поляризатора ![]() эти цвета изменяются, причем каждый из них
переходит в дополнительный цвет. Поясним это следующим примером.
На рис.6а изображена помещенная между
поляризаторами пластинка, у которой нижняя половина толще верхней.
Пусть свет, проходящий через пластину, содержит излучение только
двух длин волн:
эти цвета изменяются, причем каждый из них
переходит в дополнительный цвет. Поясним это следующим примером.
На рис.6а изображена помещенная между
поляризаторами пластинка, у которой нижняя половина толще верхней.
Пусть свет, проходящий через пластину, содержит излучение только
двух длин волн: ![]() и
и ![]() . На
рис.6б дан «вид» со стороны поляризатора
. На
рис.6б дан «вид» со стороны поляризатора ![]() .
По выходе из кристаллической пластинки каждая из составляющих
излучения будет, вообще говоря, поляризована по эллипсу.
Ориентация и эксцентриситет эллипсов для длин волн
.
По выходе из кристаллической пластинки каждая из составляющих
излучения будет, вообще говоря, поляризована по эллипсу.
Ориентация и эксцентриситет эллипсов для длин волн ![]() и
и
![]() , а также для разных половин пластинки будут различны.
, а также для разных половин пластинки будут различны.
При установке плоскости поляризатора ![]() в положение
в положение ![]() в
излучении, прошедшем через
в
излучении, прошедшем через ![]() , будет преобладать в верхней
половине пластинки длина волны
, будет преобладать в верхней
половине пластинки длина волны ![]() , в нижней половине —
, в нижней половине —
![]() . Поэтому обе половины будут иметь разную окраску. При
установке поляризатора
. Поэтому обе половины будут иметь разную окраску. При
установке поляризатора ![]() в положение
в положение ![]() окраска верхней
половины будет определяться излучением с длиной волны
окраска верхней
половины будет определяться излучением с длиной волны ![]() ,
нижней половины — излучением с длиной волны
,
нижней половины — излучением с длиной волны ![]() . Таким
образом, при повороте поляризатора
. Таким
образом, при повороте поляризатора ![]() на
на ![]() обе половины
пластинки как бы обмениваются окраской. Разумеется, так будет
обстоять дело лишь при определенном соотношении толщин обеих
частей пластинки.
обе половины
пластинки как бы обмениваются окраской. Разумеется, так будет
обстоять дело лишь при определенном соотношении толщин обеих
частей пластинки.