Рассмотрим кристаллическую пластинку, вырезанную параллельно
оптической оси. В предыдущем параграфе мы выяснили, что при
падении на такую пластинку плоскополяризованного света
обыкновенный и необыкновенный лучи оказываются когерентными. На
входе в пластинку разность фаз ![]() этих лучей равна нулю, на
выходе из пластинки
этих лучей равна нулю, на
выходе из пластинки
Вырезанная параллельно оптической оси пластинка, для которой
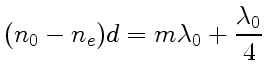
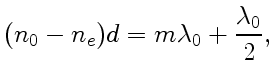
Рассмотрим прохождение плоскополяризованного света через пластинку
в полволны. Колебание
![]() в падающем луче, совершающееся
в плоскости
в падающем луче, совершающееся
в плоскости ![]() , возбудит при входе в кристалл колебание
, возбудит при входе в кристалл колебание
![]() обыкновенного луча и колебание
обыкновенного луча и колебание
![]() необыкновенного луча (рис.2).
необыкновенного луча (рис.2).
За время прохождения через пластинку разность фаз между
колебаниями
![]() и
и
![]() изменяется на
изменяется на ![]() .
Поэтому на выходе из пластинки фазовое соотношение между
обыкновенным и необыкновенным лучами будет соответствовать
взаимному расположению векторов
.
Поэтому на выходе из пластинки фазовое соотношение между
обыкновенным и необыкновенным лучами будет соответствовать
взаимному расположению векторов
![]() и
и
![]() (на входе в пластинку оно соответствовало взаимному расположению
векторов
(на входе в пластинку оно соответствовало взаимному расположению
векторов
![]() и
и
![]() ). Следовательно, свет,
вышедший из пластинки, будет поляризован в плоскости
). Следовательно, свет,
вышедший из пластинки, будет поляризован в плоскости ![]() .
Плоскости
.
Плоскости ![]() и
и ![]() расположены симметрично относительно
оптической оси пластинки
расположены симметрично относительно
оптической оси пластинки ![]() . Таким образом, пластинка в полволны
поворачивает плоскость колебаний прошедшего через нее света на
угол
. Таким образом, пластинка в полволны
поворачивает плоскость колебаний прошедшего через нее света на
угол ![]() (
(![]() угол между плоскостью колебаний в
падающем луче и осью пластинки).
угол между плоскостью колебаний в
падающем луче и осью пластинки).
Теперь пропустим плоскополяризованный свет через пластинку в
четверть волны
(рис.3).
Если расположить пластинку так, чтобы угол ![]() между
плоскостью колебаний
между
плоскостью колебаний ![]() в падающем луче и осью пластинки
в падающем луче и осью пластинки ![]() равнялся
равнялся ![]() , амплитуды обоих лучей, вышедших из пластинки,
будут одинаковы (предполагается, что дихроизма нет). Сдвиг по
фазе между колебаниями в этих лучах составит
, амплитуды обоих лучей, вышедших из пластинки,
будут одинаковы (предполагается, что дихроизма нет). Сдвиг по
фазе между колебаниями в этих лучах составит
![]() . Следовательно, свет,
вышедший из пластинки, будет поляризован по кругу. При ином
значении угла
. Следовательно, свет,
вышедший из пластинки, будет поляризован по кругу. При ином
значении угла ![]() амплитуды иышедших из пластинки лучей
будут неодинаковыми. Поэтому при наложении эти лучи образуют свет,
поляризованный по эллипсу, одна из осей которого совпадает с осью
пластинки
амплитуды иышедших из пластинки лучей
будут неодинаковыми. Поэтому при наложении эти лучи образуют свет,
поляризованный по эллипсу, одна из осей которого совпадает с осью
пластинки ![]() .
.
При пропускании плоскополяризованного света через пластинку в не
совпадающее с
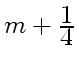 или
или
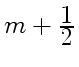 дробное число волн из
пластинки выйдут две когерентные, поляризованные во взаимно
перпендикулярных плоскостях световые волны, разность фаз которых
отличается от
дробное число волн из
пластинки выйдут две когерентные, поляризованные во взаимно
перпендикулярных плоскостях световые волны, разность фаз которых
отличается от
![]() и от
и от ![]() .
Следовательно, при любом отношении амплитуд этих волн, зависящем
от угла
.
Следовательно, при любом отношении амплитуд этих волн, зависящем
от угла ![]() (см. рис.3), на выходе из
пластинки получится эллиптически поляризованный свет, причем ни
одна из осей эллипса не будет совпадать с осью пластинки
(см. рис.3), на выходе из
пластинки получится эллиптически поляризованный свет, причем ни
одна из осей эллипса не будет совпадать с осью пластинки ![]() .
Ориентация осей эллипса относительно оси
.
Ориентация осей эллипса относительно оси ![]() определяется
разностью фаз
определяется
разностью фаз ![]() , а также отношением амплитуд, т. е. углом
, а также отношением амплитуд, т. е. углом
![]() между плоскостью колебаний в падающей волне и осью
пластинки
между плоскостью колебаний в падающей волне и осью
пластинки ![]() .
.
Отметим, что, независимо от толщины пластинки, при ![]() ,
равном нулю или
,
равном нулю или
![]() , в пластинке
будет распространяться только один луч (в первом случае
необыкновенный, во втором — обыкновенный), так что на выходе из
пластинки свет останется плоскополяризованным с плоскостью
колебаний, совпадающей с
, в пластинке
будет распространяться только один луч (в первом случае
необыкновенный, во втором — обыкновенный), так что на выходе из
пластинки свет останется плоскополяризованным с плоскостью
колебаний, совпадающей с ![]() .
.
Если на пути эллиптически поляризованного света поставить
пластинку в четверть волны, расположив ее оптической осью вдоль
одной из осей эллипса, то пластинка внесет дополнительную разность
фаз, равную
![]() . В результате
разность фаз двух плоскополяризованных волн, дающих в сумме
эллиптически поляризованную волну, станет равной нулю или
. В результате
разность фаз двух плоскополяризованных волн, дающих в сумме
эллиптически поляризованную волну, станет равной нулю или ![]() ,
так что наложение этих волн даст плоскополяризованную волну.
Следовательно, надлежащим образом повернутая пластинка в четверть
волны превращает эллиптически поляризованный свет в
плоскополяризованный. На этом основывается метод, с помощью
которого можно отличить эллиптически поляризованный свет от
частично поляризованного или свет, поляризованный по кругу, от
естественного. Исследуемый свет пропускается через пластинку в
четверть волны и помещенный за ней поляризатор. Если исследуемый
луч является эллиптически поляризованным (или поляризованным по
кругу), то, вращая пластинку и поляризатор вокруг направления
луча, удается добиться полного затемнения поля зрения. Если же
свет является частично поляризованным (или естественным), то ни
при каком положении пластинки и поляризатора невозможно получить
погашения исследуемого луча.
,
так что наложение этих волн даст плоскополяризованную волну.
Следовательно, надлежащим образом повернутая пластинка в четверть
волны превращает эллиптически поляризованный свет в
плоскополяризованный. На этом основывается метод, с помощью
которого можно отличить эллиптически поляризованный свет от
частично поляризованного или свет, поляризованный по кругу, от
естественного. Исследуемый свет пропускается через пластинку в
четверть волны и помещенный за ней поляризатор. Если исследуемый
луч является эллиптически поляризованным (или поляризованным по
кругу), то, вращая пластинку и поляризатор вокруг направления
луча, удается добиться полного затемнения поля зрения. Если же
свет является частично поляризованным (или естественным), то ни
при каком положении пластинки и поляризатора невозможно получить
погашения исследуемого луча.