Закон Бугера. Прохождение световой волны через вещество сопровождается потерей энергии этой волны, затрачиваемой на возбуждение колебаний электронов (точнее, на изменение их состояния в атоме). Частично эта энергия возвращается излучению в виде вторичных волн, порождаемых колеблющимися электронами; частично же она переходит в другие формы энергии (во внутреннюю энергию вещества).
Поэтому интенсивность света при прохождении через обычное вещество уменьшается — свет поглощается в веществе. Поглощение света можно описать с энергетической точки зрения, не вникая в механизм взаимодействия света с атомами вещества, чем мы и воспользуемся.
Пусть через однородное вещество распространяется параллельный
световой пучок. Выделим мысленно в этом веществе бесконечно тонкий
плоский слой толщины ![]() (рис.18).
(рис.18).
При прохождении этого слоя интенсивность света уменьшится так, что
ее убыль можно представить как 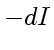 . Ясно, что эта величина будет
пропорциональна интенсивности в данном поглощающем слое и его
толщине
. Ясно, что эта величина будет
пропорциональна интенсивности в данном поглощающем слое и его
толщине ![]() , т. е.
, т. е.
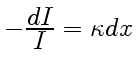 .
.
После интегрирования в пределах от ![]() до
до ![]() и от 0 до
и от 0 до ![]() найдем:
найдем:
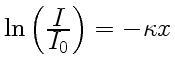 , откуда
, откуда
Заметим, что в случае точечного источника света, находящегося в
однородной поглощающей среде, предыдущие рассуждения следует
повторить, но только не для интенсивности ![]() , а для светового
потока
, а для светового
потока ![]() . И в качестве исходного бесконечно тонкого слоя
теперь следует выбрать сферический слой с радиусами от
. И в качестве исходного бесконечно тонкого слоя
теперь следует выбрать сферический слой с радиусами от ![]() до
до 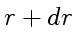 . В результате приходим к аналогичному (32)
закону:
. В результате приходим к аналогичному (32)
закону:
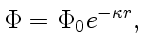
О коэффициентах поглощения. Для всех веществ поглощение
имеет селективный характер, т. е. коэффициент поглощения
![]() зависит от длины волны света (в вакууме). Для жидких и
твердых веществ зависимость
зависит от длины волны света (в вакууме). Для жидких и
твердых веществ зависимость
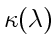 имеет вид, подобный
изображенному на рис.19.
имеет вид, подобный
изображенному на рис.19.
Т. е. сильное поглощение обнаруживается в достаточно широком интервале длин волн.
Совсем иначе ведет себя коэффициент
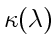 в случае
газов или паров металлов при невысоком давлении. Здесь для всех
длин волн коэффициент
в случае
газов или паров металлов при невысоком давлении. Здесь для всех
длин волн коэффициент
![]() , и лишь для очень узких
спектральных интервалов
, и лишь для очень узких
спектральных интервалов
![]() (порядка нескольких
тысячных нм) обнаруживает резкие максимумы
(рис.20). Эти максимумы соответствуют
резонансным частотам колебаний электронов внутри атомов, которые
практически не взаимодействуют друг с другом.
(порядка нескольких
тысячных нм) обнаруживает резкие максимумы
(рис.20). Эти максимумы соответствуют
резонансным частотам колебаний электронов внутри атомов, которые
практически не взаимодействуют друг с другом.
При повышении же давления максимумы поглощения все больше
расширяются, и при высоких давлениях спектр
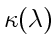 приближается к спектрам поглощения жидкостей. Это связано с ростом
взаимодействия между атомами.
приближается к спектрам поглощения жидкостей. Это связано с ростом
взаимодействия между атомами.
В заключение отметим, что можно создать такое состояние атомов
вещества, при котором коэффициент ![]() становится
отрицательным, и прохождение света через вещество в таком
(инверсионном, как говорят) состоянии сопровождается усилением его
интенсивности. Именно это и осуществляется в лазерах.
становится
отрицательным, и прохождение света через вещество в таком
(инверсионном, как говорят) состоянии сопровождается усилением его
интенсивности. Именно это и осуществляется в лазерах.