Введение. Под дифракцией света, как и других волновых процессов, понимают любое отклонение от прямолинейного распространения колебаний в среде с резкими неоднородностями (края экранов, отверстия и др.), что связано с отклонениями от законов геометрической оптики. Это приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.
Мы постоянно наблюдаем дифракцию звуковых волн, волн на
поверхности воды, радиоволн. Для наблюдения же дифракции световых
волн необходимы специальные условия, обусловленные малостью их
длин волн
![]() .
.
Наблюдение дифракции света проводят обычно по такой схеме. На пути световой волны помещают непрозрачную преграду, закрывающую часть световой волны. За преградой располагают экран, на котором при определенных условиях возникает дифракционная картина в виде той или иной системы полос и пятен — максимумов и минимумов освещенности. Исследование распределения интенсивности света на экране и будет являться основной нашей задачей, поскольку дает достаточно обширную информацию как о свойствах самой световой волны, так и о действии того или иного участка незакрытой части преграды (круглых отверстий, щелей и др.).
Первое объяснение дифракции света принадлежит Френелю (1818 г.). Он показал, что количественное описание дифракционных явлений возможно на основе построения Гюйгенса, если его дополнить принципом интерференции вторичных волн.
Вообще говоря, для описания дифракционных явлений не требуется вводить никаких новых принципов. В рамках электромагнитной теории света задача сводится к нахождению решения уравнений Максвелла при определенных граничных условиях. Однако решение такой задачи представляет большие математические трудности. Поэтому в большинстве случаев, представляющих практический интерес, вполне достаточным оказывается приближенный метод решения задачи о распределении интенсивности света, основанный на принципе Гюйгенса-Френеля. Именно этот принцип и основанные на нем простые и наглядные методы расчета мы и возьмем за основу дальнейшего изложения.
Принцип Гюйгенса-Френеля. Этот принцип является основным постулатом волновой теории, описывающим и объясняющим механизм распространения волн, в частности световых. В чем его суть?
Рассмотрим экран Э с некоторым отверстием, через которое
проходит свет от точечного монохроматического источника ![]() (рис. 7). Задача состоит в определении
напряженности
(рис. 7). Задача состоит в определении
напряженности ![]() в любой точке
в любой точке ![]() за экраном.
за экраном.
В методе Френеля предполагается, что напряженность ![]() в точках
отверстия такова, как и при отсутствии экрана, и что в точках
непосредственно за экраном
в точках
отверстия такова, как и при отсутствии экрана, и что в точках
непосредственно за экраном ![]() . Т. е. считается, что
существенна только форма отверстия экрана, но не сам экран. Это
предположение, как показал опыт, справедливо, когда размеры
отверстия и расстояния до источника и точки наблюдения
. Т. е. считается, что
существенна только форма отверстия экрана, но не сам экран. Это
предположение, как показал опыт, справедливо, когда размеры
отверстия и расстояния до источника и точки наблюдения ![]() значительно больше длины волны
значительно больше длины волны
![]() , т. е. когда отклонения
от геометрической оптики довольно малы. Оно нарушается для
отверстия, например, щели, ширина которой значительно меньше
, т. е. когда отклонения
от геометрической оптики довольно малы. Оно нарушается для
отверстия, например, щели, ширина которой значительно меньше
![]() .
.
Закроем мысленно отверстие в экране произвольной поверхностью ![]() .
Разобьем эту поверхность на элементарные участки
.
Разобьем эту поверхность на элементарные участки ![]() . По
предположению Френеля каждый из этих участков становится
источником вторичной сферической волны. Амплитуда вторичной
световой волны, достигающей интересующей нас точки
. По
предположению Френеля каждый из этих участков становится
источником вторичной сферической волны. Амплитуда вторичной
световой волны, достигающей интересующей нас точки ![]() , должна
быть пропорциональна амплитуде
, должна
быть пропорциональна амплитуде ![]() первичной волны, приходящей к
элементу
первичной волны, приходящей к
элементу ![]() , а также площади самого элемента
, а также площади самого элемента ![]() , и обратно
пропорциональна расстоянию
, и обратно
пропорциональна расстоянию ![]() от элемента
от элемента ![]() до точки
до точки ![]() .
.
Для определения результирующей амплитуды колебаний в точке ![]() , т.
е. суммы элементарных амплитуд, необходимо еще учесть, что
колебания от разных элементов
, т.
е. суммы элементарных амплитуд, необходимо еще учесть, что
колебания от разных элементов ![]() достигают точки
достигают точки ![]() с разными
фазами. Это приводит к появлению в выражении для результирующей
амплитуды множителя
с разными
фазами. Это приводит к появлению в выражении для результирующей
амплитуды множителя
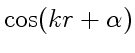 , где
, где
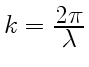 , а
, а ![]() —
дополнительная фаза, равная фазе первичной волны в элементе
—
дополнительная фаза, равная фазе первичной волны в элементе ![]() (для разных элементов она в общем случае не одинакова).
(для разных элементов она в общем случае не одинакова).
Таким образом, результирующая амплитуда напряженности ![]() в
точке
в
точке ![]() может быть представлена как суперпозиция элементарных
амплитуд с учетом их взаимных фазовых соотношений:
может быть представлена как суперпозиция элементарных
амплитуд с учетом их взаимных фазовых соотношений:
В интеграле (18) ![]() — величина, определяемая
амплитудой световой волны в месте нахождения элемента
— величина, определяемая
амплитудой световой волны в месте нахождения элемента ![]() ;
;
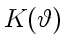 — некоторый коэффициент, зависящий от угла
— некоторый коэффициент, зависящий от угла
![]() между первоначальным направлением световой волны в
данной точке — волновым вектором
между первоначальным направлением световой волны в
данной точке — волновым вектором
![]() — и направлением на
точку
— и направлением на
точку ![]() . Естественно предположить, что коэффициент
. Естественно предположить, что коэффициент ![]() монотонно
убывает с ростом угла
монотонно
убывает с ростом угла ![]() . Многие практически важные
дифракционные задачи можно, как мы увидим далее, решить при весьма
общих предположениях относительно
. Многие практически важные
дифракционные задачи можно, как мы увидим далее, решить при весьма
общих предположениях относительно
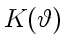 , не уточняя
конкретного вида зависимости его от угла
, не уточняя
конкретного вида зависимости его от угла ![]() .
.
В дальнейшем мы будем рассматривать ситуации, позволяющие в
качестве поверхности ![]() брать волновую поверхность падающей
волны, что значительно упрощает расчеты. В этом случае угол
брать волновую поверхность падающей
волны, что значительно упрощает расчеты. В этом случае угол
![]() в коэффициенте
в коэффициенте
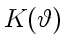 представляет собой угол
между нормалью
представляет собой угол
между нормалью
![]() к элементу поверхности
к элементу поверхности ![]() и
направлением от
и
направлением от ![]() к точке
к точке ![]() , а дополнительную фазу
, а дополнительную фазу ![]() в
(18) можно считать равной нулю,
в
(18) можно считать равной нулю,
![]() . Интеграл
(18) выражает собой математическую формулировку принципа Гюйгенса-Френеля. Суть этого принципа в следующем: для определения амплитуды колебания в точке
. Интеграл
(18) выражает собой математическую формулировку принципа Гюйгенса-Френеля. Суть этого принципа в следующем: для определения амплитуды колебания в точке ![]() , лежащей перед
некоторой поверхностью
, лежащей перед
некоторой поверхностью ![]() , надо найти амплитуды колебаний,
приходящих в эту точку от всех элементов dS поверхности S и затем
сложить их с учетом амплитуд и фаз. При этом предполагается, что
все элементы поверхности
, надо найти амплитуды колебаний,
приходящих в эту точку от всех элементов dS поверхности S и затем
сложить их с учетом амплитуд и фаз. При этом предполагается, что
все элементы поверхности ![]() взаимно когерентны — это необходимое
условие для интерференции вторичных волн.
взаимно когерентны — это необходимое
условие для интерференции вторичных волн.
Принцип Гюйгенса-Френеля можно представить в простой и наглядной форме с помощью векторной (фазовой) диаграммы (рис. 8).
Использование подобных диаграмм в дальнейшем позволит значительно
упростить многие рассуждения и расчеты. На этой диаграмме
результирующая амплитуда — вектор ![]() — представлена как
векторная сумма амплитуд
— представлена как
векторная сумма амплитуд ![]() колебаний в точке
колебаний в точке ![]() от
различных элементов
от
различных элементов ![]() поверхности
поверхности ![]() с учетом их фаз, т. е.
углов между ними.
с учетом их фаз, т. е.
углов между ними.