В 1934г. Черенков 6, работавший под руководством Вавилова 7 обнаружил особый вид свечения жидкостей под действием ![]() -лучей радия. Вавилов высказал правильное предположение, что источником излучения служат быстрые электроны, создаваемые
-лучей радия. Вавилов высказал правильное предположение, что источником излучения служат быстрые электроны, создаваемые ![]() -лучами. Это явление получило название эффекта Вавилова-Черенкова. Его полное теоретическое объяснение было дано в 1937г. Таммом 8 и Франком 9. (В 1958г. работа Черенкова, Тамма и Франка была отмечена Нобелевской премией.)
-лучами. Это явление получило название эффекта Вавилова-Черенкова. Его полное теоретическое объяснение было дано в 1937г. Таммом 8 и Франком 9. (В 1958г. работа Черенкова, Тамма и Франка была отмечена Нобелевской премией.)
Согласно электромагнитной теории заряд, движущийся равномерно, не
излучает электромагнитных волн (см. И.В.Савельев ``Курс общей
физики'' кн.2 § 2.6). Однако, как показали Тамм и Франк, это
справедливо лишь в том случае, если скорость ![]() заряженной
частицы не превышает фазовую скорость
заряженной
частицы не превышает фазовую скорость
![]() электромагнитных волн в той среде, в
которой движется частица. При условии, что
электромагнитных волн в той среде, в
которой движется частица. При условии, что
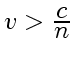 , даже двигаясь равномерно, частица
излучает электромагнитные волны. В действительности частица теряет
энергию на излучение, вследствие чего движется с отрицательным
ускорением. Но это ускорение является не причиной (как в случае
, даже двигаясь равномерно, частица
излучает электромагнитные волны. В действительности частица теряет
энергию на излучение, вследствие чего движется с отрицательным
ускорением. Но это ускорение является не причиной (как в случае
 ), а следствием
излучения. Если бы потеря энергии за счет излучения восполнялась
каким-либо способом, то частица, движущаяся равномерно со
скоростью
), а следствием
излучения. Если бы потеря энергии за счет излучения восполнялась
каким-либо способом, то частица, движущаяся равномерно со
скоростью
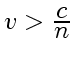 , все равно
была бы источником излучения.
, все равно
была бы источником излучения.
Эффект Вавилова-Черенкова наблюдался экспериментально для электронов, протонов и мезонов при движении их в жидких и твердых средах.
В излучении Вавилова-Черенкова преобладают короткие волны, поэтому оно имеет голубую окраску. Наиболее характерным свойством этого излучения является то, что оно испускается не по всем направлениям, a лишь вдоль образующих конуса, ось которого совпадает с направлением скорости частицы (рис.21).
Угол ![]() между направлениями распространения излучения и
вектором скорости частицы определяется соотношением
между направлениями распространения излучения и
вектором скорости частицы определяется соотношением
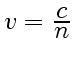 . Поэтому черенковские счетчики позволяют
не только регистрировать частицы, но и судить об их энергии.
Удается даже определить угол
. Поэтому черенковские счетчики позволяют
не только регистрировать частицы, но и судить об их энергии.
Удается даже определить угол